The four most common Maxwell relations
The four most common Maxwell relations are the equalities of the second derivatives of each of the four thermodynamic potentials, with respect to their thermal natural variable (temperature T or entropy S ) and their mechanical natural variable (pressure p or volume V ):
where the potentials as functions of their natural thermal and mechanical variables are:
 - The internal energy
- The internal energy - The Enthalpy
- The Enthalpy - The Helmholtz free energy
- The Helmholtz free energy - The Gibbs free energy
- The Gibbs free energy
Derivation of the Maxwell relations
Derivation of the Maxwell equations can be deduced from the differential forms of the thermodynamic potentials:
These equations resemble total differentials of the form
And indeed, it can be shown that for any equation of the form
that
Consider, as an example, the equation  . We can now immediately see that
. We can now immediately see that
Since we also know that for functions with continuous second derivatives, the mixed partial derivatives are identical, that is, that
we therefore can see that
and therefore that
Each of the four Maxwell relationships given above follows similarly from one of the Gibbs equations.
General Maxwell relationships
The above are by no means the only Maxwell relationships. When other work terms involving other natural variables besides the volume work are considered or when the number of particles is included as a natural variable, other Maxwell relations become apparent. For example, if we have a single-component gas, then the number of particles N is also a natural variable of the above four thermodynamic potentials. The Maxwell relationship for the enthalpy with respect to pressure and particle number would then be:
where μ is the chemical potential. In addition, there are other thermodynamic potentials besides the four that are commonly used, and each of these potentials will yield a set of Maxwell relations.
Each equation can be re-expressed using the relationship
which are sometimes also known as Maxwell relations.








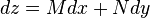











No comments:
Post a Comment